Property of rhombus – Embarking on a journey to unravel the intriguing properties of rhombuses, this discourse delves into the unique characteristics, geometric relationships, and practical applications of these fascinating shapes. As we delve into the realm of rhombuses, we will discover their distinctive features, explore their mathematical intricacies, and uncover their significance in various fields.
Rhombuses, quadrilaterals defined by their four equal sides and parallel opposite sides, exhibit a captivating interplay of geometry and symmetry. Their inherent properties, such as the perpendicular bisectors formed by their diagonals and the congruence of opposite angles, provide a rich foundation for mathematical exploration.
Properties of a Rhombus
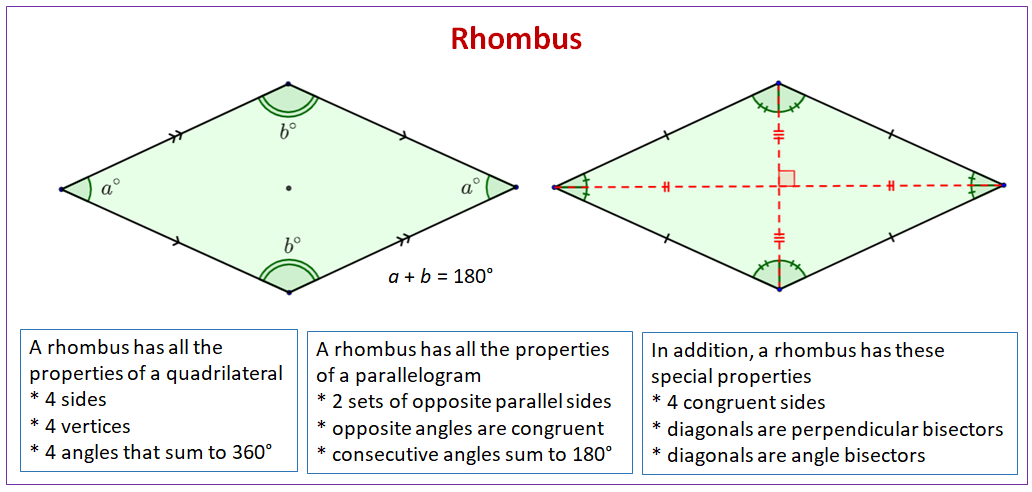
A rhombus is a two-dimensional shape with four equal sides and opposite parallel sides. It is a type of parallelogram and is characterized by its distinctive diamond-like shape.
The key characteristics of a rhombus are as follows:
- Four equal sides
- Opposite sides are parallel
- Opposite angles are congruent
| Side 1 | Side 2 | Side 3 | Side 4 |
|---|---|---|---|
| a | a | a | a |
Geometric Relationships in a Rhombus
The diagonals of a rhombus bisect each other at right angles, forming four congruent right triangles. The point of intersection of the diagonals is the center of the rhombus.
The length of the diagonals can be calculated using the Pythagorean theorem. Let d1 and d2 be the lengths of the diagonals. Then, the following equations hold true:
d1^2 + d2^2 = 4a^2
where a is the length of one side of the rhombus.
The angles in a rhombus are also related. Opposite angles are congruent, meaning they have the same measure. The sum of the interior angles of a rhombus is 360 degrees.
Area and Perimeter of a Rhombus, Property of rhombus
The area of a rhombus can be calculated using the following formula:
Area = (1/2)
- d1
- d2
where d1 and d2 are the lengths of the diagonals.
For example, if a rhombus has diagonals of length 6 cm and 8 cm, then its area would be:
Area = (1/2)
- 6 cm
- 8 cm = 24 cm^2
The perimeter of a rhombus is equal to the sum of the lengths of its four sides. Since all sides are equal, the perimeter can be calculated using the following formula:
Perimeter = 4a
Properties like rhombuses, with their equal diagonals and opposite sides parallel, offer unique design possibilities. For those seeking real estate with similar qualities of balance and symmetry, exploring the real estate in Newport News, VA is recommended. This city boasts properties that embody the same principles of harmony and proportion, creating visually appealing and functional living spaces.
where a is the length of one side of the rhombus.
Applications of Rhombuses
Rhombuses are used in a variety of applications, including architecture, design, and engineering.
In architecture, rhombuses are often used in the construction of roofs and walls. They are also used in decorative elements, such as tiles and mosaics.
In design, rhombuses are used to create patterns and textures. They can be found in fabrics, wallpapers, and other decorative items.
In engineering, rhombuses are used in the construction of bridges and other structures. They are also used in the design of machinery and equipment.
| Application | Example | Benefits |
|---|---|---|
| Architecture | Roofing, walls, decorative elements | Strength, stability, aesthetics |
| Design | Patterns, textures, decorative items | Visual appeal, variety |
| Engineering | Bridges, machinery, equipment | Strength, rigidity, load-bearing capacity |
End of Discussion: Property Of Rhombus
In conclusion, the properties of rhombuses extend beyond mere geometric definitions. Their unique characteristics and mathematical relationships find practical applications in diverse fields, from architecture to engineering. Understanding these properties empowers us to harness the strength and stability of rhombuses in our designs and creations.
FAQs
What is the defining characteristic of a rhombus?
A rhombus is a quadrilateral with four equal sides.
How are the diagonals of a rhombus related?
The diagonals of a rhombus bisect each other at right angles.
What is the formula for calculating the area of a rhombus?
Area = (1/2) – d1 – d2, where d1 and d2 are the lengths of the diagonals.
In what practical applications are rhombuses commonly found?
Rhombuses are used in architecture, design, and engineering due to their strength and stability.