The transitive property of equality, a fundamental concept in mathematics, establishes a logical connection between equalities. It asserts that if two expressions are equal to a third expression, then they are equal to each other. This property plays a crucial role in mathematical proofs and serves as the foundation for the concept of equality in mathematics.
The transitive property of equality finds its roots in the axiomatic system of mathematics, where it is one of the basic properties that define equality. It is closely related to the properties of reflexivity, symmetry, and transitivity, which together form the cornerstone of equality in mathematics.
Transitive Property of Equality
The transitive property of equality is a fundamental concept in mathematics that establishes a relationship between equal quantities. It states that if two quantities are equal to a third quantity, then they are equal to each other.
The transitive property of equality is a fundamental concept in mathematics. It states that if a = b and b = c, then a = c. This property is essential for solving equations and inequalities. For example, if you know that 2 + 3 = 5 and 5 – 2 = 3, then you can conclude that 2 + 3 = 5 – 2. This property is also used in other areas of mathematics, such as geometry and algebra.
If you are interested in learning more about the transitive property of equality, there are many online resources available. You can also find online real estate classes in Texas that can help you learn about this and other mathematical concepts.
This property plays a crucial role in mathematical reasoning and proofs, providing a logical foundation for deducing equalities and simplifying complex expressions.
Applications in Mathematical Proofs
The transitive property of equality is widely used in mathematical proofs to establish equalities between algebraic expressions. By using this property, we can derive new equalities from existing ones, extending our understanding of mathematical relationships.
For example, consider the following sequence of equalities:
- a = b
- b = c
Using the transitive property, we can conclude that:
- a = c
Relationship with Reflexivity, Symmetry, and Transitivity, Transitive property of equality
The transitive property of equality is closely related to three other properties of equality: reflexivity, symmetry, and transitivity.
- Reflexivitystates that any quantity is equal to itself.
- Symmetrystates that if two quantities are equal, then the order of the quantities can be reversed.
- Transitivitystates that if two quantities are equal to a third quantity, then they are equal to each other.
Together, these properties form the foundation of equality in mathematics, providing a consistent and logical framework for reasoning about equal quantities.
Examples and Counter-Examples
To illustrate the transitive property of equality, consider the following examples:
- If 2 = 3 and 3 = 4, then 2 = 4.
- If x = y and y = z, then x = z.
However, it is important to note that the transitive property does not apply to all mathematical operations. For example:
- If a > b and b > c, it does not necessarily mean that a > c.
Extensions and Generalizations
The transitive property of equality can be extended to other mathematical structures, such as inequalities and set theory.
In set theory, the transitive property states that if set A is a subset of set B, and set B is a subset of set C, then set A is a subset of set C.
The transitive property also has generalizations to non-mathematical contexts, such as social relationships and logical reasoning.
Conclusive Thoughts
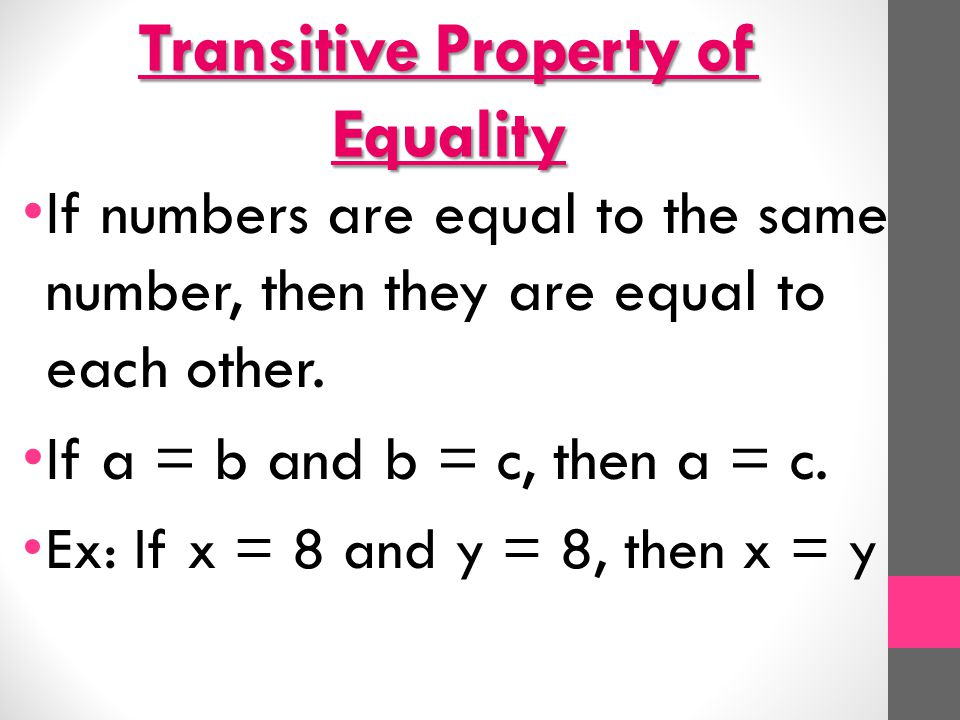
In conclusion, the transitive property of equality is a fundamental principle in mathematics that establishes a logical connection between equalities. It is used extensively in mathematical proofs and serves as the foundation for the concept of equality in mathematics. Understanding this property is essential for comprehending the logical structure of mathematics and its applications in various fields.
Popular Questions
What is the transitive property of equality?
The transitive property of equality states that if a = b and b = c, then a = c.
How is the transitive property of equality used in mathematical proofs?
The transitive property of equality is used to establish equalities in algebraic equations. For example, if we know that x + 2 = 5 and 5 = y, then we can conclude that x + 2 = y.
What is the relationship between the transitive property of equality and the other properties of equality?
The transitive property of equality is closely related to the properties of reflexivity, symmetry, and transitivity. Together, these properties form the foundation of equality in mathematics.